Question

Hello, Can anyone help me, please!

I need it done by tonight. Is my homework. Is due today! I'm struggling.
(Please show your work please thanks <3)

Answer 1

Explanation:

46. The midsegment Theorem states that a line segment connecting the midpoints of the legs of the trapezoid is parallel to the bases, and equal to half their sum.

Using this info,

We already know EF=11 so

`(1)/(2) (8 + 2x - 4) = 11`

`x + 2 = 11`

`x = 9`

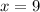
53. Apply Midpoint Formula

`( (x1 + x2)/(2) \: and \: (y1 + y2)/(2) )`

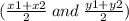
Let find the midpoint of each side

KL (+2a/2, +2a/2), LM(-2a/2, 2a/2) MN(-2a/2, -2a/2) NK(2a/2, -2a/2)

So the midpoint of each side is

KL=(a,a)

LM= (-a,a)

MN=(-a,-a)

NK=(a,-a).

The slopes of these line is y2-y1/x2-x1

KL=2a/-2a=-a

LM=-2a/-2a=a

MN=-2a/2a=-a

NK=-2a/-2a=a

Let find the length of all sides. Since each coordinate has a form of 0 in it, we would just consider the finite value, 2a.

Distance of all sides are 2a.

Consider the midpoint, notice how each midpoint can be obtained by a rotation of 90-180-270 or 360 degrees about the origin of one of the midpoints. Since all the side lengths and slope are equal, a rigid transformation like a rotation would preserve the side lengths and midpoint of each line. It also proves rotational symmetry and the only 4 figure quadralaterial that has a 90,180,270, and/or 360 degrees rotational symmetry is a square.