Question

Suppose A = B"Cm, where A has the dimensions LT, B has dimensions L²T-1, and C has dimensions LT2. Then the exponents n and have the values

Answer 1

Complete Question:

Suppose
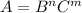`A = B^n C^m`, where A has the dimensions LT, B has dimensions L²T⁻¹, and C has dimensions LT². Then the exponents n and m have the values

Answer:

The value of n = ¹/₅

The value of m = ³/₅

Step-by-step explanation:

Given dimensions;

A = LT

B = L²T⁻¹

C = LT²

The values of n and m are calculated as follows;

`LT = [L^2T^(-1)]^n[LT^2]^m\\\\L^1T^1 = [L^(2n)T^(-n)]* [L^mT^(2m)]\\\\L^1 * T^1 = [L^((2n+m))] * [T^((-n +2m))]\\\\1 = 2n + m -----(1)\\\\1 = -n + 2m ----(2)\\\\from \ (1); \ m = 1-2n, \ \ substitute \ the \ value \ of \ m \ in\ (2)\\\\1= -n +2(1-2n)\\\\1 = -n + 2-4n\\\\1-2 = -5n\\\\-1 = -5n\\\\1= 5n\\\\n = (1)/(5) \\\\m = 1 - 2n\\\\m = 1 - 2((1)/(5) )\\\\m = 1- (2)/(5) \\\\m = (3)/(5)`