Question

[LOOK AT THE PICTURE]

I can't understand why it can be written as

`(1)/(2) {x}^{ (1)/(2) - 1}`
PLS ANS CLEARLY​

Answer 1

The rule is

`(d)/(dx)x^n = nx^(n-1)`

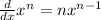
which is the power rule. You pull down the exponent to place it as the coefficient. So that explains the 1/2 pull out front. Then we subtract 1 from the exponent.

The expression you wrote can be simplified or rewritten like this

`(d)/(dx)x^n = nx^(n-1)\\\\(d)/(dx)\left[x^(1/2)\right] = (1)/(2)x^{(1)/(2)-1}\\\\(d)/(dx)\left[x^(1/2)\right] = (1)/(2)x^{-(1)/(2)}\\\\(d)/(dx)\left[x^(1/2)\right] = (1)/(2)\frac{1}{x^{(1)/(2)}}\\\\(d)/(dx)\left[x^(1/2)\right] = \frac{1}{2x^{(1)/(2)}}\\\\(d)/(dx)\left[x^(1/2)\right] = (1)/(2√(x))}\\\\`

Optionally, we can multiply top and bottom by
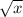`√(x)` to rationalize the denominator.