Question

The average high temperature during the hottest month in Beijing, China, is 72°F. The average high temperature during the coldest month in Beijing is 18°F. The function t = 27 cosine (StartFraction pi Over 6 EndFraction (m minus 6)) + 45, where m represents the number of months after January, models the temperature throughout the year in Beijing. During which month in the year would the temperature reach 55°F? August September November December

Answer 1

B. September

Explanation:

Correct on Edge 2021

Answer 2

During the month of September.

Explanation:

The temperature in Beijing, in m months after January, is given by the following equation:

`T(m) = 27\cos{((\pi)/(6)(m-6))} + 45`

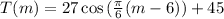
In which m is the number of months after January.

During which month in the year would the temperature reach 55°F?

We have to find m for which: T(m) = 55. So

`T(m) = 27\cos{((\pi)/(6)(m-6))} + 45`

`55 = 27\cos{((\pi)/(6)(m-6))} + 45`

`27\cos{((\pi)/(6)(m-6))} = 10`

`\cos{((\pi)/(6)(m-6))} = (10)/(27)`

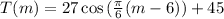
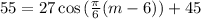
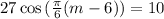
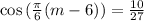
Applying the inverse cosine to both sides:

`\cos^(-1){(\cos{((\pi)/(6)(m-6))})} = \cos^(-1){((10)/(27))}`

`(\pi)/(6)(m-6) = 1.19`

`\pi(m-6) = 6*1.19`

`\pi m - 6\pi = 6*1.19`

`\pi m = 6*1.19 + 6\pi`

`m = (6*1.19 + 6\pi)/(\pi)`

`m = 8.27`

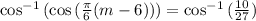
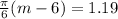
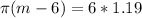
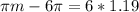
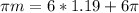
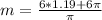
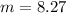
8.27 months after January

8.27 + 1 = 9.27, so during the month of September.