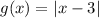Question

30. f(x) = |x|; reflection in the y-axis followed by a
translation 3 units right

Answer 1

`g(x) = |x-3|`

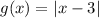
Explanation:

We are given the parent function:

`f(x) = |x|`

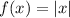
And we want to find the equation after a reflection in the y-axis followed by a translation of three units right.

To reflect a function over the y-axis, we multiply the input by a negative. That is:

`\displaystyle f(x) \rightarrow f(-x)`

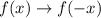
In other words, a reflection over the y-axis will be given by:

`f(-x) = |-x|`

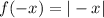
To shift horzontally, we add if we are moving leftwards or subtract if we are moving rightwards. That is:

`f(x) \rightarrow f(x-k)`

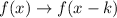
Where k is the horizontal translation.

Since we are translating three units rightwards, k = 3. Hence:

`\displaystyle f(-(x-3)) = |-(x-3)|`

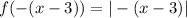
Recall that |ab| = |a||b|. Hence:

`\displaystyle f(-(x-3)) = |-(x-3)| = |-1||(x-3)| = |x-3|`

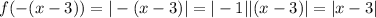
Hence, f reflected over the y-axis followed by a translation of three units right is given by:

`g(x) = |x-3|`