Question

An expression is shown below:

f(x) = 2x² − x − 10

Part A: What are the x-intercepts of the graph of f(x)? Show your work. (2 points)

Part B: Is the vertex of the graph of f(x) going to be a maximum or minimum? What are the coordinates of the vertex? Justify your answers and show your work. (3 points)

Part C: What are the steps you would use to graph f(x)? Justify that you can use the answers obtained in Part A and Part B to draw the graph. (5 points)

(10 points)

Answer 1

Part A

`2x^2 -x-10=0\\\\(x+2)(2x-5)=0\\\\x=-2, (5)/(2)`

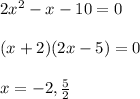
So, the x-intercepts are (-2,0) and (5/2, 0).

Part B

The vertex will be a minimum because the leading coefficient of the quadratic is positive, meaning the graph will open up.

The vertex has an x-coordinate that is the average of the roots, which in this case is 1/4.

`f(1/4)=-81/8`

So, the coordinates of the vertex are
`\left((1)/(4), -(81)/(8) \right)`

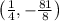
Part C

Plot the two x-intercepts and the vertex. Then, draw a parabola through these points that opens up.