Question

What is the value of y in the sequence below?
2,y,18, -54,162,

Answer 1

First, let's check if the sequence is geometric or arithmetric.

If arithmetric, the sequence will have common difference.

Arithmetric

`\displaystyle \large{a_(n + 1) - a_n = d}`

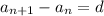
d stands for a common difference. Common Difference means that sequences must have same difference after subtracting.

Geometric

`\displaystyle \large{ (a_(n + 1))/(a_n) = r}`

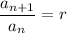
r stands for a common ratio.

To find the value of y, you can check the sequence. If we try subtracting the sequences, the differences are different. That means the sequences are not arithmetric. That only leaves the geometric sequence.

Let's check by dividing sequences.

We have:

• 2,y,18,-54,162,...

Let's check by divide -54 by 18 and 162 by -54. We need to divide more than one so we can prove that the sequence is geometric.

`\displaystyle \large{ ( - 54)/(18) = - 3 } \\ \displaystyle \large{ ( 162)/( - 54) = - 3}`

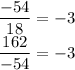
Hence, the sequence is geometric.

Because the common ratio is -3. Let these be the following:

`\displaystyle \large{ a_(n + 1) = y } \\ \displaystyle \large{ a_n = 2 } \\ \displaystyle \large{ r = - 3 }`

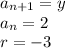
From the:

`\displaystyle \large{ (a_(n + 1))/(a_n) = r}`

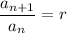
Substitute the values in.

`\displaystyle \large{ (y)/(2) = - 3}`

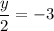
Multiply the whole equation by 2 to isolate y.

`\displaystyle \large{ (y)/(2) * 2 = - 3 * 2} \\ \displaystyle \large{ y = - 6}`

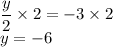
Therefore, the value of y is -6.