Question

{-2, -2/7, 0, 0.3, √7, 7.1, √64}

a. List all the natural numbers from the given set.

b. List all the whole numbers from the given set.

c. List all the integers from the given set.

d. List all the rational numbers from the given set.

e. List all the irrational numbers from the given set.

f. List all the real numbers from the given set.

Answer 1

Answers:

• a) √64
• b) 0, √64
• c) -2, 0, √64
• d) -2, -2/7, 0, 0.3, 7.1, √64
• e) √7
• f) -2, -2/7, 0, 0.3, √7, 7.1, √64

==========================================================

Explanations:

Part (a)

The set of natural numbers is {1,2,3,4,...} which is the set of positive whole numbers. We don't include 0. Note that
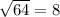`√(64) = 8` to show that it's part of the set of natural numbers. Something like -2 is not in the set, same for -2/7, etc.

------------------------------

Part (b)

The set of whole numbers is {0,1,2,3,...} which is almost identical to the previous set, but we're now including 0.

------------------------------

Part (c)

The set of integers is {..., -3, -2, -1, 0, 1, 2, 3, ...}

We are including the negative values as well as the positive values too. Zero is included.

------------------------------

Part (d)

Any rational number is of the form p/q, where p,q are integers and q is nonzero. Something like -2/7 is rational. Here we have p = -2 and q = 7.

Any whole number is rational. Eg: 8 = 8/1

Any decimal that terminates is rational. The value 7.1 is the same as 71/10

------------------------------

Part (e)

If a number isn't rational, then it's considered irrational.

Something like
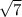`√(7)` is irrational because 7 isn't a perfect square.

The decimal version of the number
`√(7) \approx 2.6457513110646` goes on forever without any pattern. So this is more evidence it's irrational.

------------------------------

Part (f)

If your teacher hasn't covered imaginary or complex numbers, then every value you encounter so far is a real number.