Question

Find the linear function f if f^-1(2)=-1 and f^-1 (-9)=3

Answer 1

`\displaystyle f(x) = -(11)/(4)(x + 1) + 2`

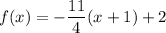
Explanation:

We want to find the linear function given that:

`f^(-1)(2) = -1\text{ and } f^(-1) (-9) = 3`

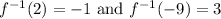
Recall that by the definition of inverse functions:

`\displaystyle \text{If } f(a) = b\text{ then } f^(-1)(b) = a`

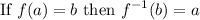
In other words, f(-1) = 2 and f(3) = -9.

This yields two points: (-1, 2) and (3, -9).

Find the slope of the linear function:

`\displaystyle m = (\Delta y)/(\Delta x) = ((-9) - (2))/((3) -(-1)) = -(11)/(4)`

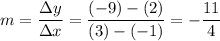
From point-slope form:

`\displaystyle y - (2) = -(11)/(4)( x- (-1))`

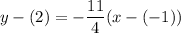
Hence:

`\displaystyle f(x) = -(11)/(4)(x + 1) + 2`

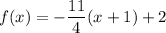
We can simplify if desired:

`\displaystyle f(x) = -(11)/(4)x -(3)/(4)`