Given the PMF
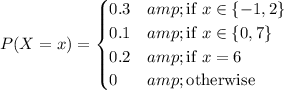
(a)
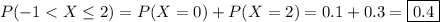
(b) The CDF is defined as
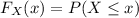 , so that
, so that

It follows that
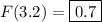
(c) Expectation is defined as
![E[X] = \displaystyle \sum_x x\,P(X=x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/q8m1huy34o286068x5ru3n.png)
We have
![E[X] = \displaystyle \sum_{x\in\{-1,0,2,6,7\}} x\,P(X=x) \\\\ E[X] = -P(X=-1) + 2P(X=2)+6P(X=6)+7P(X=7) \\\\ E[X] = -0.3 + 0.6 + 1.2 + 0.7 = \boxed{2.2}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/owsraop0i35oh2a9ek099v.png)
(d) First compute the second moment of X, which is defined as
![E[X^2] = \displaystyle \sum_x x^2\,P(X=x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/1lnkc2nlafbeeyot1hzcbo.png)
We get
![E[X^2] = (-1)^2P(X=-1) + 2^2P(X=2) + 6^2P(X=6) + 7^2P(X=7) \\\\ E[X^2] = 0.3 + 1.2 + 7.2 + 4.9 = 13.6](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/xqbc21w7vn8vj074clsjdt.png)
Variance is defined as
![\mathrm{Var}[X] = E[(X - E[X])^2] = E[X^2] - E[X]^2](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/o20nr5fuvvjxbkxk6soqks.png)
so it follows that
![\mathrm{Var}[X] = 13.6 - 2.2^2 = \boxed{8.76}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/9bf5oy7sna9c1s7neuhfqs.png)
(e) Not sure what this part has to do with the rest of the question. At any rate, if Y is a random variable following a Poisson distribution with λ = 3, then Y has a PDF of
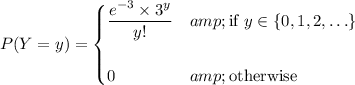
Then
