Question

Shreya left the hardware store and drove toward the train station. One hour later Jill left driving 13 km/h faster in an effort to catch up to her. After five hours Jill finally caught up. What was Shreya's average speed?​

Answer 1

65 km/h

Explanation:

We know that

Distance = Speed × Time

Let,

Speed = x

Now,

Distance after 1 hr

=> x × 1

=> x

Distance after 5 hr

=> x × 5

=> 5x

Total distance = 5x + x = 6x

Now,

Total speed = (x + 13) × 5

=> 5x + 65

Now,

Avg. speed

=> 6x = 5x + 65

=> 6x - 5x = 65

=> x = 65

Therefore

Average speed of Shreya = 65 km/h

Answer 2

Shreya's average speed was 65 kilometers per hour.

Explanation:

Let the average speed of Shreya be r.

Recall that the distance d traveled is given by the equation:

`\displaystyle d = rt`

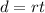
Where r is the speed and t is the time (in this case hours).

After one hour, when Jill left, Shreya would have already traveled:

`\displaystyle d = r(1) = r\text{ km}`

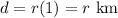
Only r kilometers.

Jill caught up in five hours. Hence, Shreya would've traveled another:

`\displaystyle d = r(5) = 5r\text{ km}`

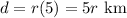
Therefore, in the six hours, Shreya traveled a total distance of:

`\displaystyle r + 5r = 6r\text{ km}`

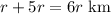
Jill drove at a speed of 13 km/hr faster than Shreya's speed. She drove for five hours. Hence, Jill's total distance traveled is represented by:

`\displaystyle d = (r + 13)\cdot 5 = 5(r+13)`

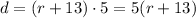
This must be equivalent to Shreya's total distance traveled as Jill caught up to her. Hence:

`\displaystyle 5(r+13) = 6r`

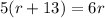
Solve for r:

`\displaystyle \begin{aligned} 5(r+13) &= 6r \\ 5r + 65 &= 6r \\ r&= 65\end{aligned}`

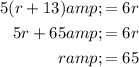
In conclusion, Shreya's average speed was 65 kilometers per hour.