Two-variable equations/single-variable functions
When some variable depends in some way or another on another variable or variables, we say that it's a function of those other variables. In the simplest case, we can have a function of a single variable. The relationship "y is twice as big as x" describes y as a function of x, and we can express it with the function y = 2x. A graph of this function requires two dimensions, with one axis for each variable (see the first picture). Notice that while y is a function of a single variable, it's a part of an equation in two variables.
Three-variable equations/two-variable functions
Let's take a look at an equation of three variables - for this example, the equation
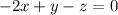. Currently, this is an example of an implicit function; there's a relationship between the variables, but the equation's form doesn't favor any one in particular. To make this a function, we can add z to both sides, giving us the new equation:
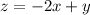
Here, z is now a function of both x and y. We can pick whatever value we'd like for x and y, and those choices will fix a certain value of z. For instance, picking x = 1 and y = 2 gives us
.
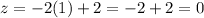To graph this function, we now need 3 dimensions and 3 axes: an x-axis, a y-axis, and z-axis. See the second photo for a graph of this function.
TL;DR: An equation in three variables can be represented as a function by solving for one of the variables, and graphed in three dimensions, with one axis for each variable.