Answer:
Point-slope form:
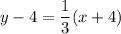
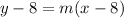
Slope-intercept form:
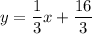
Standard form:
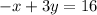
Explanation:
Hi there!
1) Point-slope form
Point-slope form:
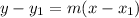 where
where
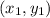 is a point on the line and m is the slope
is a point on the line and m is the slope
First, determine the slope:
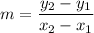 where two points on the line are
where two points on the line are
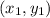 and
and
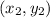
Plug in the points (-4,4) and (8,8):

Therefore, the slope of the line is
 . Plug this into
. Plug this into
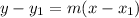 :
:
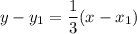
Now, for
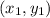 , we can either plug in (-4,4) or (8,8):
, we can either plug in (-4,4) or (8,8):

or
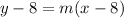
2) Slope-intercept form
Slope-intercept form:
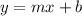 where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
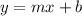
Plug in the slope

Now, to determine the y-intercept, plug in one of the points (-4,4) or (8,8) and solve for b:
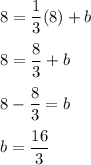
Therefore, the y-intercept is
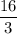 . Plug this back into
. Plug this back into
 :
:
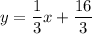
3) Standard form
Standard form:
 where A, B, and C are numbers which are typically integers
where A, B, and C are numbers which are typically integers
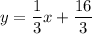
Organize this into standard form:
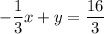
Multiply both sides by 3 so A, B, and C are integers:
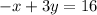
I hope this helps!