Question

12. Elmo is standing on a parade float tossing candy out to everyone. The candy is thrown with a starting velocity of 10

feet per second from a height of 3 feet modeled by the equation: h= -16t2 + 10t + 3

After how many seconds will the ball be 2 feet in the air?

a. 0.125

b. 0.5

c. 0.71

d. 0.625

Answer 1

c. 0.71

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

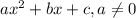This polynomial has roots
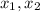`x_(1), x_(2)` such that
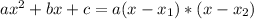`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\Delta))/(2*a)`

`x_(2) = (-b - √(\Delta))/(2*a)`

`\Delta = b^(2) - 4ac`

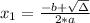
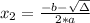
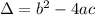
The height of the candy after t seconds is given by the following equation:

`h(t) = -16t^2 + 10t + 3`

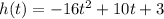
After how many seconds will the ball be 2 feet in the air?

This is t for which
`h(t) = 2`

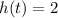
So

`h(t) = -16t^2 + 10t + 3`

`2 = -16t^2 + 10t + 3`

`-16t^2 + 10t + 1 = 0`

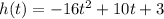
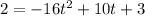
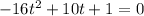
So

`a = -16, b = 10, c = 1`

`\Delta = b^(2) - 4ac = 10^2 -4(-16)(1) = 164`

`t_(1) = (-10 + √(164))/(2*(-16)) = -0.09`

`t_(2) = (-10 - √(164))/(2*(-16)) = 0.71`

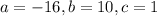
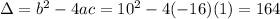
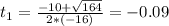
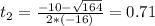
Since time is a positive measure, the answer is 0.71, which is option c.