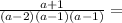Question

Perform the indicated operation. Simplify the result in factored form.

Answer 1

The Answer That I Had Got Is… a+7/(a+1)(a-1)(a-2)

Answer 2

`(a+1)/((a-2)(a-1)(a-1))=`

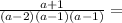
Explanation:

1. Approach

The easiest method to solve this problem is to factor the expression. In order to subtract (or add) two fractions, both fractions have to have common denominators. When the fractions are factored one can easily see the least common denominator. Convert both fractions to the least common denominator by multiplying the numerator (number over the fraction bar) and denominator (number under the fraction bar) by the value such that both fractions have the same denominator. Finally, one can subtract the numerators of the two fractions.

2. Factoring and Least common denominator

`(3)/(a^2-3a+2)-(2)/(a^2-1)=`

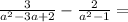
Factor the expression, rewrite the quadratic polynomials as the product of two linear polynomials,

`(3)/(a^2-3a+2)-(2)/(a^2-1)=`

`(3)/((a-2)(a-1))-(2)/((a-1)(a+1))=`

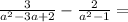
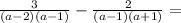
The least common denominator is: (
`(a-2)(a-1)(a-1)`)

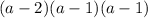Convert both fractions to the least common denominator, multiply both the numerator and denominator by the same value to do so,

`(3)/((a-2)(a-1))-(2)/((a-1)(a+1))=`

`(3)/((a-2)(a-1))*(a-1)/(a-1)-(2)/((a-1)(a+1))*(a-2)/(a-2)=`

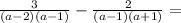
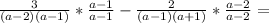
Simplify,

`(3)/((a-2)(a-1))*(a-1)/(a-1)-(2)/((a-1)(a+1))*(a-2)/(a-2)=`

`(3(a-1))/((a-2)(a-1)(a-1))-(2(a-2))/((a-1)(a+1)(a-2))=`

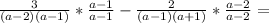
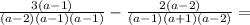
3. Solving the expression

`(3(a-1))/((a-2)(a-1)(a-1))-(2(a-2))/((a-1)(a+1)(a-2))=`

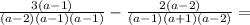
Distribute, multiply every term inside the parenthesis by the term outside of it,

`(3(a-1))/((a-2)(a-1)(a-1))-(2(a-2))/((a-1)(a+1)(a-2))=`

`(3a-3)/((a-2)(a-1)(a-1))-(2a-4)/((a-1)(a+1)(a-2))=`

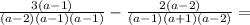
Simplify further,

`(3a-3)/((a-2)(a-1)(a-1))-(2a-4)/((a-1)(a+1)(a-2))=`

`(3a-3-(2a-4))/((a-2)(a-1)(a-1))=`

`(3a-3-2a+4)/((a-2)(a-1)(a-1))=`

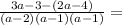
Combine like terms,

`(3a-3-2a+4)/((a-2)(a-1)(a-1))=`

`(a+1)/((a-2)(a-1)(a-1))=`