Well let's say that to compare these two numbers, we have to start with the definition first.
Definition
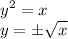
Looks like we can use any x-values right? Nope.
The value of x only applies to any positive real numbers for one reason.
As we know, any numbers time itself will result in positive. No matter the negative or positive.
Definition II
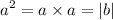
Where b is the result from a×a. Let's see an example.
Examples
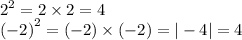
So basically, their counterpart or opposite still gives same value.
Then you may have a question, where does √-1 come from?
It comes from this equation:
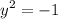
When we solve the quadratic equation in this like form, we square both sides to get rid of the square.
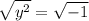
Then where does plus-minus come from? It comes from one of Absolute Value propety.
Absolute Value Property I
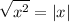
Solving absolute value always gives the plus-minus. Therefore...
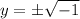
Then we have the square root of -1 in negative and positive. But something is not right.
As I said, any numbers time itself of numbers squared will only result in positive. So how does the equation of y^2 = -1 make sense? Simple, it doesn't.
Because why would any numbers squared result in negative? Therefore, √-1 does not exist in a real number system.
Then we have another number which is -√1. This one is simple.
It is one of the solution from the equation y^2 = 1.
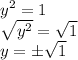
We ignore the +√1 but focus on -√1 instead. Of course, we know that numbers squared itself will result in positive. Since 1 is positive then we can say that these solutions exist in real number.
Conclusion
So what is the different? The different between two numbers is that √-1 does not exist in a real number system since any squared numbers only result in positive while -√1 is one of the solution from y^2 = 1 and exists in a real number system.