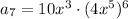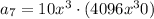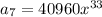Answer:
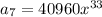
Explanation:
Geometric sequence has explicit form:
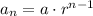 where
where
 is first term and
is first term and
 is the common ratio.
is the common ratio.
First term here is
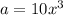 and
and
 could be found by doing second term divided by first term,
could be found by doing second term divided by first term,
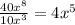 .
.
Therefore the
 th term is given by
th term is given by
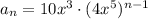 .
.
So the
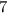 th term is given by
th term is given by
 .
.
Let's simplify: