Answer:
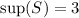 .
.
 .
.
Explanation:
When factored,
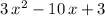 is equivalent to
is equivalent to
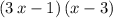 .
.
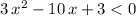 whenever
whenever
 .
.
Typically, the supremum and infimum of open intervals are the two endpoints. In this question,
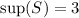 whereas
whereas
 .
.
Below is a proof of the claim that
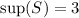 . The proof for
. The proof for
 is similar.
is similar.
In simple words, the supremum of a set is the smallest upper bound of that set. (An upper bound of a set is greater than any element of the set.)
It is easy to see that
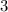 is an upper bound of
is an upper bound of
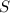 :
:
- For any
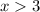 ,
,
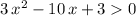 . Hence, any number that's greater than
. Hence, any number that's greater than
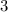 could not be a member
could not be a member
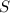 .
. - Conversely,
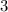 would be greater than all elements of
would be greater than all elements of
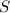 and would thus be an upper bound of this set.
and would thus be an upper bound of this set.
To see that
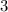 is the smallest upper bound of
is the smallest upper bound of
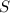 , assume by contradiction that there exists some
, assume by contradiction that there exists some
 for which
for which
 (which is smaller than
(which is smaller than
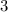 ) is also an upper bound of
) is also an upper bound of
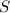 .
.
The next step is to show that
 could not be a lower bound of
could not be a lower bound of
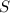 .
.
There are two situations to consider:
- The value of
 might be very large, such that
might be very large, such that
 is smaller than all elements of
is smaller than all elements of
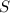 .
. - Otherwise, the value of
 ensures that
ensures that
 .
.
Either way, it would be necessary to find (or construct) an element
 of
of
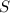 such that
such that
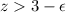 .
.
For the first situation, it would be necessary that
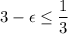 , such that
, such that
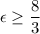 . Let
. Let
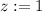 (or any other number between
(or any other number between
 and
and
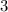 .)
.)
- Apparently
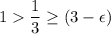 .
.
- At the same time,
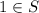 .
.
- Hence,
 would not be an upper bound of
would not be an upper bound of
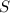 when
when
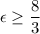 .
.
With the first situation
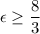 accounted for, the second situation may assume that
accounted for, the second situation may assume that
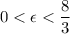 .
.
Claim that
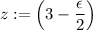 (which is strictly greater than
(which is strictly greater than
 ) is also an element of
) is also an element of
 .
.
- To verify that
 , set
, set
 and evaluate the expression:
and evaluate the expression:
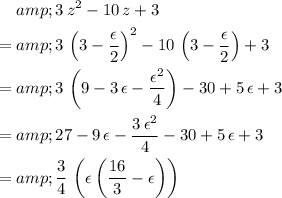 .
. - This expression is smaller than
 whenever
whenever
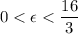 .
. - The assumption for this situation
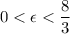 ensures that
ensures that
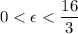 is indeed satisfied.
is indeed satisfied. - Hence,
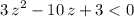 , such that
, such that
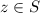 .
. - At the same time,
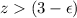 . Hence,
. Hence,
 would not be an upper bound of
would not be an upper bound of
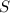 .
.
Either way,
 would not be an upper bound of
would not be an upper bound of
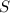 . Contradiction.
. Contradiction.
Hence,
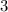 is indeed the smallest upper bound of
is indeed the smallest upper bound of
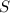 . By definition,
. By definition,
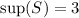 .
.
The proof for
 is similar and is omitted because of the character limit.
is similar and is omitted because of the character limit.