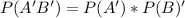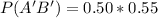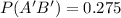Question

A manufacturing company has two retail outlets. It is known that 40% of all potentialcustomers buy products from outlet 1 alone, 35% buy from outlet 2 alone, and 10% buy fromboth 1 and 2. LetAdenote the event that a potential customer, randomly chosen, buys fromoutlet 1, and letBdenote the event that the customer buys from outlet 2. Suppose a potentialcustomer is chosen at random. For each of the following events, represent the eventsymbolically and then find its probability.

Required:
a. The customer buys from outlet 1.
b. The customer does not buy from outlet 2.
c. The customer does not buy from outlet 1 or does not buy from outlet 2.
d. The customer does not buy from outlet 1 and does not buy from outlet 2.

Answer 1

`P(A) = 0.50`

`P(B') = 0.55`

`P(A' U B') = 0.775`

`P(A'B') = 0.275`

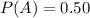
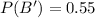
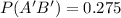
Step-by-step explanation:

Given

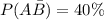`P(A\bar B) = 40\%` --- From outlet 1 alone

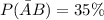`P(\bar A B) = 35\%` --- From outlet 2 alone

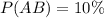`P(AB) = 10\%` --- From both

Solving (a): Buys from outlet 1;

This is represented as: P(A) and the solution is:

`P(A) = P(A\bar B) + P(A B)`

`P(A) = 40\% + 10\%`

`P(A) = 50\%`

`P(A) = 0.50`

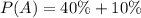
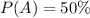
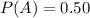
Solving (b): Does not buy from outlet 2;

This is represented as: P(B') :

First, calculate the probability that the customer buys from 2

`P(B) = P(\bar AB) + P(A B)`

`P(B) = 35\% + 10\%`

`P(B) = 45\%`

`P(B) = 0.45`

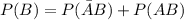
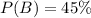
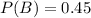
Using the complement rule, we have:

`P(B') = 1 - P(B)`

`P(B') = 1 - 0.45`

`P(B') = 0.55`

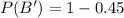
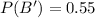
Solving (c): Does not buy from 1 or does not buy from 2

This is represented as:
`P(A' U B')`

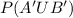
And the solution is:

`P(A' U B') = P(A') + P(B') - P(A'B')`

`P(A' U B') = P(A') + P(B') - P(A') * P(B')`

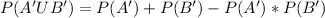
Using complement rule:

`P(A') = 1 - P(A)`

`P(A') = 1 - 0.50`

`P(A') = 0.50`

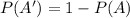
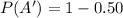
The equation becomes:

`P(A' U B') = 0.50 + 0.55 - 0.50 * 0.55`

`P(A' U B') = 0.775`

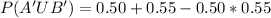
Solving (d): Does not buy from 1 or does not buy from 2

This is represented as:

`P(A'B')`

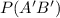
And it is calculated as:

`P(A'B') = P(A') * P(B)'`

`P(A'B') = 0.50 * 0.55`

`P(A'B') = 0.275`