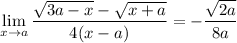Question

Plz with steps plzzzzzz

Answer 1

Answer:
`-(√(2a))/(8a)`

=======================================================

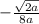
Step-by-step explanation:

The (x-a) in the denominator causes a problem if we tried to simply directly substitute in x = a. This is because we get a division by zero error.

The trick often used for problems like this is to rationalize the numerator as shown in the steps below.

`\displaystyle \lim_(x\to a) (√(3a-x)-√(x+a))/(4(x-a))\\\\\\\lim_(x\to a) ((√(3a-x)-√(x+a))(√(3a-x)+√(x+a)))/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\\lim_(x\to a) ((√(3a-x))^2-(√(x+a))^2)/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\\lim_(x\to a) (3a-x-(x+a))/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\\lim_(x\to a) (3a-x-x-a)/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\`

`\displaystyle \lim_(x\to a) (2a-2x)/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\\lim_(x\to a) (-2(-a+x))/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\\lim_(x\to a) (-2(x-a))/(4(x-a)(√(3a-x)+√(x+a)))\\\\\\\lim_(x\to a) (-2)/(4(√(3a-x)+√(x+a)))\\\\\\`

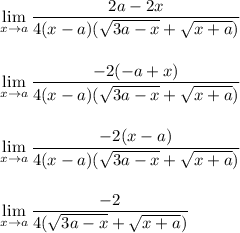
At this point, the (x-a) in the denominator has been canceled out. We can now plug in x = a to see what happens

`\displaystyle L = \lim_(x\to a) (-2)/(4(√(3a-x)+√(x+a)))\\\\\\L = (-2)/(4(√(3a-a)+√(a+a)))\\\\\\L = (-2)/(4(√(2a)+√(2a)))\\\\\\L = (-2)/(4(2√(2a)))\\\\\\L = (-2)/(8√(2a))\\\\\\L = (-1)/(4√(2a))\\\\\\L = (-1*√(2a))/(4√(2a)*√(2a))\\\\\\L = (-√(2a))/(4√(2a*2a))\\\\\\L = (-√(2a))/(4√((2a)^2))\\\\\\L = (-√(2a))/(4*2a)\\\\\\L = -(√(2a))/(8a)\\\\\\`

There's not much else to say from here since we don't know the value of 'a'. So we can stop here.

Therefore,

`\displaystyle \lim_(x\to a) (√(3a-x)-√(x+a))/(4(x-a)) = -(√(2a))/(8a)\\\\\\`