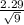Answer:
Population mean = 7 ± 2.306 ×
Explanation:
Given - A university researcher wants to estimate the mean number
of novels that seniors read during their time in college. An exit
survey was conducted with a random sample of 9 seniors. The
sample mean was 7 novels with standard deviation 2.29 novels.
To find - Assuming that all conditions for conducting inference have
been met, which of the following is a 94.645% confidence
interval for the population mean number of novels read by
all seniors?
Proof -
Given that,
Mean ,x⁻ = 7
Standard deviation, s = 2.29
Size, n = 9
Now,
Degrees of freedom = df
= n - 1
= 9 - 1
= 8
⇒Degrees of freedom = 8
Now,
At 94.645% confidence level
α = 1 - 94.645%
=1 - 0.94645
=0.05355 ≈ 0.05
⇒α = 0.5
Now,
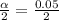
= 0.025
Then,
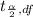 = 2.306
= 2.306
∴ we get
Population mean = x⁻ ±
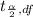 ×
×
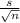
= 7 ± 2.306 ×
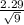
⇒Population mean = 7 ± 2.306 ×