Question

Consider the following series.

1/6 + 1/12 + 1/18 + 1/24 + 1/30

Determine whether the series is convergent or divergent. Justify your answer.

a. Converges; the series is a constant multiple geometric series.
b. Converges; the limit of the terms, an, is 0 as n goes to infinity.
c. Diverges; the limit of the terms, an, is not 0 as n goes to infinity.
d. Diverges; the series is a constant multiple of the harmonic series.

If it is convergent, find the sum.

Answer 1

d. Diverges; the series is a constant multiple of the harmonic series.

Explanation:

Given

`Series: (1)/(6) + (1)/(12) + (1)/(18) + (1)/(24) + (1)/(30) + ...`

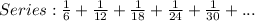
Required

Determine if it diverges or converges

From the series, we have:

`T_1 = (1)/(6) = (1)/(6 * 1)`

`T_2 = (1)/(12) = (1)/(6 * 2)`

`T_3 = (1)/(18) = (1)/(6 * 3)`

`T_4 = (1)/(24) = (1)/(6 * 4)`

`T_5 = (1)/(30) = (1)/(6 * 5)`

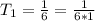
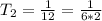
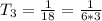
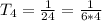
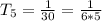
So, each term can be written as:

`T_n = (1)/(6n)`

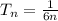
And the series is:

`\limits^\infty_1\sum T_n = \limits^\infty_1\sum (1)/(6n)`

`\limits^\infty_1\sum T_n = (1)/(6) * \limits^\infty_1\sum (1)/(n)`

`\limits^\infty_1\sum T_n = (1)/(6) * \infty`

`\limits^\infty_1\sum T_n = \infty`

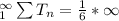
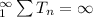
Recall that:

`\limits^\infty_1\sum (1)/(n)` is known as the harmonic series, and it diverges to infinity

Hence: (d) is correct