Question

5. Based on the graph of the trigonometric function,
what is the amplitudes

Answer 1

`\displaystyle 3`

Step-by-step explanation:

`\displaystyle y = Asin(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \\ Amplitude \hookrightarrow |A|`

AND

`\displaystyle y = Acos(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \\ Amplitude \hookrightarrow |A|`

Accourding to the graph AND the above information, your amplitude is three units. This means each crest is extended three units beyond the midline of
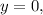`\displaystyle y = 0,` the centre of your graph, also known as the vertical shift. So, no matter how far the graph shifts vertically, the midline will ALWAYS follow.

Now, just in case you wanted to know the equation(s) of this graph, look below:

`\displaystyle y = 3sin\:((\pi)/(2)x + (\pi)/(2)) \\ y = 3cos\:(\pi)/(2)x`

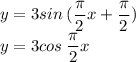
I am delighted to assist you at any time.

Answer 2

Amplitude is 3 from 0-3 or 0 to -3