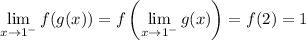Recall some limit properties…
• limits distribute over sums:
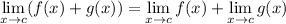
• limits distribute over products:
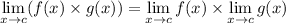
• limits distribute over quotients, provided that the denominator doesn't approach 0 :
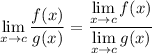
• if f(x) is continuous at x = c, then the limit "passes through" a composition:
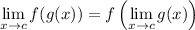
# # #
(a) This limit is 2. At x = 2, we have f (2) = 1, but from either side of x = 2, we see f(x) approaching the point (2, 2). So
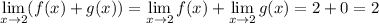
(b) This limit does not exist. We would have
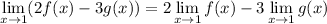
but g(x) approaches 2 from the left of x = 1, and g(x) approaches 1 from the right of x = 1. The one-sided limits don't match, so the two-sided limit doesn't exist.
(c) This limit is 0. It looks like f(x) passes through the origin, while g(x) ≈ 3/2 at x = 0. So
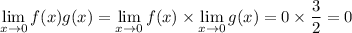
(d) This limit does not exist since

(e) This limit is 16. Nothing tricky here, just use the same property as in (c).
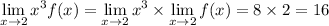
(f) This limit is 1. f(x) is continuous at x = 1, while g(x) approaches 2 from the left.