Question

When a 360 nF air capacitor is connected to a power supply, the energy stored in the capacitor is 1.85 x 10-5 J. While the capacitor is kept connected to the power supply, a slab of dielectric is inserted that completely fills the space between the plates. This increases the stored energy by 2.32 x 10-5 J. (a) What is the potential difference between the capacitor plates

Answer 1

(a) Approximately
`10.1\; {\rm V}`.

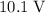Step-by-step explanation:

Let
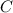`C` denote the capacitance of a capacitor. Let
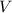`V` be the potential difference (voltage) between the two plates of this capacitor. The energy
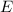`E` stored in this capacitor would be:

`\displaystyle E = (1)/(2)\, C\, (V^(2))`.

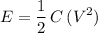Rearrange this equation to find an expression for the potential difference
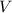`V` in terms of capacitance
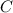`C` and energy
`E`:

`\begin{aligned}V^(2) &= (2\, E)/(C) \end{aligned}`.

`\begin{aligned}V &= \sqrt{(2\, E)/(C)} \end{aligned}`

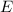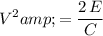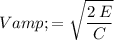
The capacitance
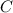`C` of this capacitor is given in nanofarads. Convert that unit to standard unit (farads):

`\begin{aligned}C &= 360\; {\rm nF} \\ &= 360\; {\rm nF} * \frac{1\; {\rm F}}{10^(9)\; {\rm nF}} \\ &= 3.60 * 10^(-7)\; {\rm F}\end{aligned}`.

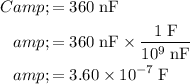Given that the energy stored in this capacitor is
`E = 1.85 * 10^(-5)\; {\rm J}`, the potential difference across the capacitor plates would be:

`\begin{aligned}V &= \sqrt{\frac{2 * 1.85 * 10^(-5)\; {\rm J}}{3.60 * 10^(-7)\; {\rm F}}} \\ &\approx 10.1\; {\rm V}\end{aligned}`.