Question

The parent exponential function of f(x)=2x has been transformed in the following ways:

-a vertical compression by a scale factor of 13
-a vertical translation of 3 units up
-and a horizontal translation of 3 units to the left

Answer 1

The resulting expression is
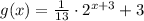`g(x) = (1)/(13)\cdot 2^(x+3)+3`. We include the graph of both functions, the red line represents the parent exponential function, whereas the blue line is for the resulting function.

Explanation:

Statement is incomplete. The question is missing. We infer that question is: What is the resulting expression? Let
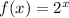`f(x) = 2^(x)`, each operation is defined below:

Vertical compression

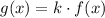`g(x) = k\cdot f(x)`, where
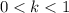`0 < k < 1`. (1)

Vertical translation upwards

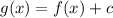`g(x) = f(x) + c`, where
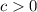`c > 0`. (2)

Horizontal translation leftwards

`g(x) = f(x+b)`,
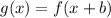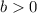`b > 0`. (3)

Now, we proceed to transform the parent exponential function:

(i) A vertical compression by a scale factor of 13 (
`k = (1)/(13)`)

`f'(x) = (1)/(13)\cdot 2^(x)`

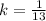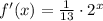
(ii) Vertical translation of 3 units up

`f'' (x) = (1)/(13)\cdot 2^(x) + 3`

(iii) Horizontal translation of 3 units to the left

`g(x) = (1)/(13)\cdot 2^(x+3)+3`

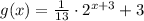
The resulting expression is
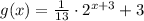`g(x) = (1)/(13)\cdot 2^(x+3)+3`. We include the graph of both functions, the red line represents the parent exponential function, whereas the blue line is for the resulting function.