Answer:
The coordinates are
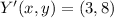 and
and
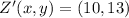 .
.
Explanation:
First, we have to derive an expression for translation under the assumption that each point of XYZ experiments the same translation. Vectorially speaking, translation from X to X' is defined by:
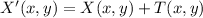 (1)
(1)
Where
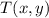 is the vector translation.
is the vector translation.
If we know that
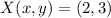 and
and
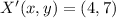 , then the vector translation is:
, then the vector translation is:
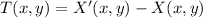
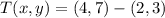
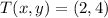
Then, we determine the coordinates for Y' and Z':
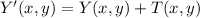
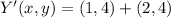
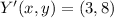
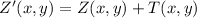
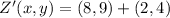
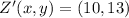
The coordinates are
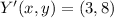 and
and
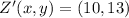 .
.