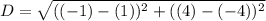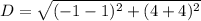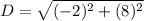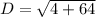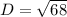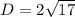Answer:
1.
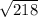
2.
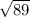
3.
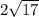
Explanation:
The formula to find the distance between any two points on a coordinate plane is as follows:
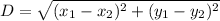
Where (
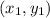 ) and (
) and (
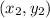 ) are the two points one is trying to find the distance between. Substitute the points in and solve for the distance between them for each respective problem.
) are the two points one is trying to find the distance between. Substitute the points in and solve for the distance between them for each respective problem.
1.
Points:
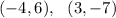
Substitute into the formula,
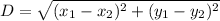
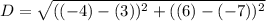
Simplify,
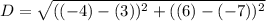
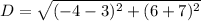
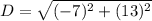
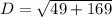
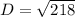
2.
Points:
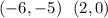
Substitute into the formula,
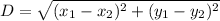
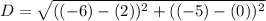
Simplify,
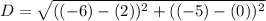
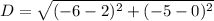
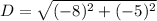
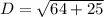
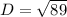
3.
Points:
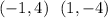
Substitute into the formula,
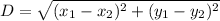
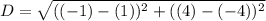
Simplify,