Question

What is an equation of the line that passes through the points (0,7) and (5,4? Put your answer in fully reduced form.

Answer 1

Answer (assuming it can be in slope-intercept format):

`y = -(3)/(5) x+7`

Explanation:

When knowing the y-intercept of a line and its slope, we can write an equation representing it in slope-intercept form, or
`y = mx + b`.

1) First, find the slope of the equation. Use the slope formula,
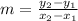`m = (y_2-y_1)/(x_2-x_1)`, to find the slope. Substitute the x and y values of the given points into the formula and simplify:

`m = ((4)-(7))/((5)-(0)) \\m = (4-7)/(5-0) \\m = (-3)/(5)`

Thus, the slope is
`-(3)/(5)`.

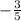2) Usually, we would have to use one of the given points and the slope to put the equation in point-slope form. However, notice that the point (0,7) has an x-value of 0. All points on the y-axis have an x-value of 0, thus (0,7) must be the y-intercept of the line. Now that we know the slope of the line and its y-intercept, we can already write the equation in slope-intercept format, represented by the equation
`y = mx + b`. Substitute
`m` and
`b` for real values.

Since
`m` represents the slope, substitute
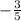`-(3)/(5)` in its place in the equation. Since
`b` represents the y-intercept, substitute 7 in its place. This gives the following equation and answer:

`y = -(3)/(5) x+7`