Question

(A) x^2 + 6x + 9 = 0

(B) 8x^2+ 5x - 6 = 0


(C) (x + 4)^2 - 36 = 0

Answer 1

Query (A)

`{ \rm{ {x}^(2) + 6x + 9 = 0 }} \\ { \rm{(x + 3)(x - 1) = 0}} \\ { \boxed{ \rm{x = {}^( - )3 \: \: and \: \: 1 }}}`

Query (B)

`{ \rm{ {8x}^(2) + 5x - 6 = 0}} \\ \\ { \rm{x = \frac{ - b \pm \sqrt{ {b}^(2) - 4ac } }{2a} }} \\ \\ { \rm{x = ( - 5 \pm √(217) )/(16) }} \\ \\ { \boxed{ \rm{ \: x = 0.608 \: \: and \: \: {}^( - ) 1.233}}}`

Query (C)

`{ \rm{ {(x + 4)}^(2) - 36 = 0 }} \\ \\ { \rm{ {(x + 4)}^(2) = 36 }} \\ \\ { \rm{x + 4 = \pm6}} \\ \\ { \boxed{ \rm{x = 2 \: \: and \: \: {}^( - ) 10}}}`

Answer 2

solution given:

(A) x^2 + 6x + 9 = 0

doing middle term

x^2+ (3+3)x+9=0

x^2 +3x+3x +9=0

taking common from two each term.

x(x+3)+3(x+3)=0

(x+3)(x+3)=0

either

x+3=0

x=-3

(B) 8x^2+ 5x - 6 = 0

Comparing above equation with

ax^2+bx+c=0,

we get,

a=8

b=5

c=-6

now

we have

`x=(-b +- √(b^2-4ac))/(2a)`

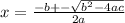
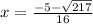
now substituting value:

`x=(-5+-√(5^2-4*8*-6) )/(2*8)`

`x=(-5+-√(217))/(16)`

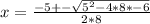
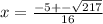
taking positive

`x=(-5+√(217))/(16)`

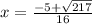
taking negative

`x=(-5-√(217))/(16)`

(C) (x + 4)^2 - 36 = 0

(x + 4)^2 - 6^2 = 0

it is in the form of x²+y²:(x+y)(x-y)

so (x + 4)^2 - 6^2 can be written as (x+4+6)(x+4-6)

above equation becomes

(x+10)(x-2)=0

either

x=-10

or

x=2

Explanation: