Answer:
So the amplitude is 7
The period is pi
The phase shift is negative pi/2
The midline is -3
Explanation:
A trigonometric function is the same as
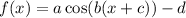
Where a is the amplitude, 2 pi/ absolute value of b is the period, c is the phase shift, and d is the vertical shift or midline.
Given the function
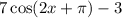
The amplitude is 7, and the midline is -3. The period is
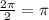
The phase shift is
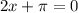

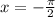
So the amplitude is 7
The period is pi
The phase shift is negative pi/2
The midline is -3.