Question

Find the distance between the two points rounding to the nearest tenth (if necessary).

(0,-6) and (9,-1)

Answer 1

Hey there! I'm happy to help!

Imagine the line that is created when you connect the two points (the distance between the two points).

You can create a right triangle where this distance is the hypotenuse where the two legs are the change in x and y. So, if you take those changes in x and y, you can use the Pythagorean Theorem (a²+b²=c²) to find the distance between the two points, which is the hypotenuse.

Our change in x is 9 because 9-0 is 9.

We square it

9²=81

Our change in y is 5 as -1-(-6) or -1+6 is 5.

5²=25

We add these.

81+25=106

We square root and round to the nearest tenth.

√106≈10.3

So, our distance is 10.3.

This Pythagorean Theorem method actually gives us a formula called the distance formula that you can use to find the distance between points.

`\sqrt{(x_(2) -x_(1))^2+(y_(2)-y_(1))^2}`

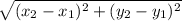
Have a wonderful day and keep on learning! :D