Question

A. 0
B. Nonexistent
C. 1
D. -1

Answer 1

Without resorting to L'Hopital's rule, recall that

`\displaystyle \lim_(x\to0)(\sin(ax))/(ax) = 1`

for a ≠ 0. Then

`\displaystyle \lim_(x\to0^+) (x \ln(x))/(\tan(x)) = \lim_(x\to0^+)\frac x{\sin(x)} * \lim_(x\to0^+)\cos(x) * \lim_(x\to0^+)\ln(x)`

The first two limits exist and are equal to 1, but the last limit is -∞.

Answer 2

`\displaystyle \lim_(x\rightarrow 0^(+)) (x\ln x)/(\tan x)=-\infty\implies \text{B. Nonexistent (best answer)}`

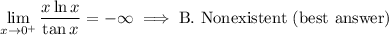
Explanation:

Recall L'Hopital's rule:

`\displaystyle \lim_(x\rightarrow c)(f(x))/(g(x))=\lim_(x\rightarrow c)(f'(x))/(g'(x))`

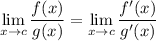
First derivative of
`x\ln x`:

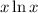Recall the product rule:

`(f\cdot g)'=f'\cdot g+g'\cdot f`

`\displaystyle (d)/(dx) (x\ln x)=(d)/(dx)(x)\cdot \ln (x)+(d)/(dx)(\ln x)\cdot x`

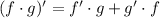
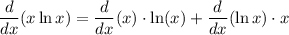
Note that:

`\displaystyle (d)/(dx)(x)=1,\\(d)/(dx)(\ln (x))=(1)/(x)`

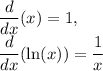
Simplifying, we get:

`\displaystyle (d)/(dx) (x\ln x)=1\cdot \ln x+(1)/(x)\cdot x,\\(d)/(dx)(x\ln x)=\ln x+1`

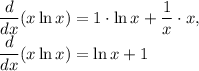
First derivative of
`\tan x`:

`\displaystyle (d)/(dx)(\tan x)=\sec^2 x`

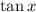Therefore, we have:

`\displaystyle \lim_(x\rightarrow 0^(+))(x\ln x)/(\tan x)=\lim_(x\rightarrow 0^(+))\frac{\ln x+1}{\sec^2{x}}`

By definition,
`\cos x=(1)/(\sec x)`. Therefore,

`\displaystyle \lim_(x\rightarrow 0^(+))(x\ln x)/(\tan x)=\lim_(x\rightarrow 0^(+))\frac{\ln x+1}{\sec^2{x}}=\lim_(x\rightarrow 0^(+))\cos^2x(\ln x+1)`

Note:

`\displaystyle \lim_(x\rightarrow 0^(+))\cos^2x=1,\\\lim_(x\rightarrow 0^(+))\ln x+1=-\infty`

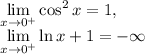
Substitute:

`\displaystyle \lim_(x \rightarrow0^(+)) \cos^2x(\ln x+1)=1\cdot (-\infty)=-\infty`

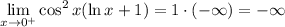
Therefore, we have:

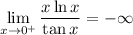`\displaystyle \lim _(x\rightarrow 0^(+))(x\ln x)/(\tan x)=-\infty \text{}`, which best corresponds with
`\boxed{\text{B. Nonexistent}}`

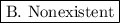
*Commentary:

Technically speaking, a limit exists only if it is equal to a real number. By proper definition, infinity is not a number. With that being said, you will see limits expressed as infinity or negative infinity.

Here's what I will say about this specific problem.

The problem is stipulating that we approach
`x` from the right side. Because of this condition, it may be unorthodox to say this limit doesn't exist. However, if the problem just asked for
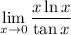`\displaystyle \lim_(x\rightarrow 0)(x\ln x)/(\tan x)`, it is common and preferred to say this limit does not exist, since
`\displaystyle \lim_(x\rightarrow 0^(-))(x\ln x)/(\tan x)\\eq \displaystyle \lim_(x\rightarrow 0^(+))(x\ln x)/(\tan x)`.

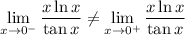For example,
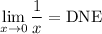`\displaystyle \lim_(x\rightarrow 0)(1)/(x)=\text{DNE}`, because
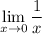`\displaystyle \lim_(x\rightarrow 0)(1)/(x)` diverges. In other words,
`\displaystyle \lim_(x\rightarrow 0^(-))(1)/(x)=-\infty \\eq \displaystyle \lim_(x\rightarrow 0^(+))(1)/(x)=\infty`.

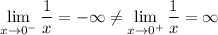But again, the problem is asking for the limit as
`x` approaches from the right, in which case
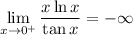`\displaystyle \lim _(x\rightarrow 0^(+))(x\ln x)/(\tan x)=-\infty }`. It's really a pedagogical choice whether to say a limit equal to infinity or negative infinity exists or not since infinity implies there is no limit, so saying the limit of something is infinity becomes an oxymoron. In this case, the person who wrote the answer choices chose to express a limit of infinity as nonexistent, but it is worth mentioning that someone else solving this problem might express
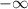`-\infty` as the answer, and they would be just as, if not more, correct.