Question

What is the perimeter of CDE?

A. 37.8 units
B. 39 units
C. 32.5 units
D. 35.6 units

Answer 1

Answer: 32.5 units (choice C)

This value is approximate.

=============================================================

Step-by-step explanation:

To find the perimeter, we simply add up the lengths of the three external sides.

The horizontal side from D to E is 16 units long since |-10-6| = 16. I subtracted the x coordinates of the points and applied absolute value. You could also count out the spaces and you should count 16 spaces from D to E.

Unfortunately, the diagonal lengths aren't as straight forward. We have two options here: The pythagorean theorem, or the distance formula.

I'll go with the distance formula.

Let's find the distance from C to D, aka the length of side CD

`C = (x1,y1) = (-1,-2)\\\\D = (x2,y2) = (-10,0)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-1-(-10))^2 + (-2-0)^2)\\\\d = √((-1+10)^2 + (-2-0)^2)\\\\d = √((9)^2 + (-2)^2)\\\\d = √(81 + 4)\\\\d = √(85)\\\\d \approx 9.2195\\\\`

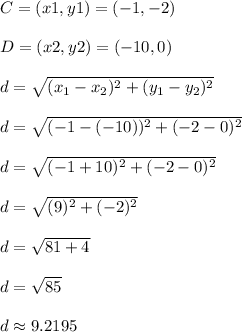
Side CD is roughly 9.2195 units long.

Repeat this idea to find the length of CE

`C = (x1,y1) = (-1,-2)\\\\E = (x2,y2) = (6,0)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-1-6)^2 + (-2-0)^2)\\\\d = √((-7)^2 + (-2)^2)\\\\d = √(49 + 4)\\\\d = √(53)\\\\d \approx 7.2801\\\\`

Side CE is roughly 7.2801 units long

The perimeter of triangle CDE is approximately...

P = DE+CD+CE

P = 16 + 9.2195 + 7.2801

P = 32.4996

This then rounds to 32.5 units. The answer is choice C.