Question

The half life of a certain tranquilizer in the bloodstream is 36 hours. How long will it take for the drug to decay to 87% of the original dose? Use the exponential decay model to solve.

Answer 1

Finding the Decay constant(λ):

λ = 0.693 / (half-life)

we are given that the half-life is 36 hours

λ = 0.693 / (36)

λ = 0.01925 /hour

Time taken for 87% decay:

Since decay is first-order, we will use the formula:

`t = (2.303)/(decay constant)log((A_0)/(A) )`

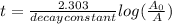
Where A₀ is the initial amount and A is the final amount

Let the initial amount be 100 mg,

the final amount will be 87% of 100

Final amount = 100*87/100 = 87 mg

Replacing the values in the equation:

`t = (2.303)/(0.01925)log((100)/(87) )`

`t = (2.303)/(0.01925)*0.06`

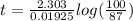
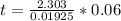
t = 7.18 hours

We used 'hours' as the unit because the unit of the decay constant is '/hour'

Therefore, the drug will decay to 87% of initial dosage after 7.18 hours