Question

Answer the question with explanation;​

Answer 1

`\displaystyle \sum^(\infty)_(n = 1) (n^2)/((n + 1)^2) = \text{div}`

General Formulas and Concepts:

Calculus

Limits

• Special Limit Rule [Coefficient Power Method]:
  `\displaystyle \lim_(x \to \pm \infty) (ax^n)/(bx^n) = (a)/(b)`

Series Convergence Tests

• nth Term Test:
  `\displaystyle \sum^(\infty)_(n = 1) a_n \rightarrow \lim_(n \to \infty) a_n`
• Integral Test:
  `\displaystyle \sum^(\infty)_(n = a) f(n) \rightarrow \int\limits^(\infty)_a {f(x)} \, dx`
• P-Series:
  `\displaystyle \sum^(\infty)_(n = 1) (1)/(n^p)`
• Direct Comparison Test (DCT)
• Limit Comparison Test (LCT)
• Alternating Series Test (AST)
• Ratio Test:
  `\displaystyle \sum^(\infty)_(n = 0) a_n \rightarrow \lim_(n \to \infty) \bigg| (a_(n + 1))/(a_n) \bigg|`

Explanation:

*Note:

Always apply the nth Term Test as the first test to use for convergence.

Rules:

1. If
   `\displaystyle \lim_(n \to \infty) S_n = 0`, then the nth Term Test is inconclusive.
2. If
   `\displaystyle \lim_(n \to \infty) S_n = l` (some number l), then the series is divergent by the nth Term Test.

Step 1: Define

Identify

`\displaystyle \sum^(\infty)_(n = 1) (n^2)/((n + 1)^2)`

Step 2: Find Convergence

1. Substitute in variables [nth Term Test]:
   `\displaystyle \sum^(\infty)_(n = 1) (n^2)/((n + 1)^2) \rightarrow \lim_(n \to \infty) (n^2)/((n + 1)^2)`
2. Expand:
   `\displaystyle \lim_(n \to \infty) (n^2)/((n + 1)^2)= \lim_(n \to \infty) (n^2)/(n^2 + 2n + 1)`
3. Evaluate limit [Special Limit Rule - Coefficient Power Method]:
   `\displaystyle \lim_(n \to \infty) (n^2)/((n + 1)^2) = 1`
4. Compute [nth Term Test]:
   `\displaystyle \sum^(\infty)_(n = 1) (n^2)/((n + 1)^2) = \text{div}`

∴ by the nth Term Test, the series diverges.

Topic: AP Calculus BC (Calculus I + II)

Unit: Convergence Tests

Answer 2

The statement in the question is wrong. The series actually diverges.

Explanation:

We compute

`\lim_(n\to\infty)(n^2)/((n+1)^2)=\lim_(n\to\infty)\left((n^2)/(n^2+2n+1)\cdot(1/n^2)/(1/n^2)\right)=\lim_(n\to\infty)\frac1{1+2/n+1/n^2}=\frac1{1+0+0}=1\\e0`

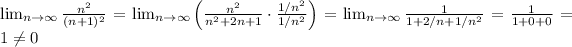
Therefore, by the series divergence test, the series
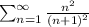`\sum_(n=1)^\infty(n^2)/((n+1)^2)` diverges.

EDIT: To VectorFundament120, if
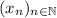`(x_n)_(n\in\mathbb N)` is a sequence, both
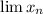`\lim x_n` and
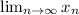`\lim_(n\to\infty)x_n` are common notation for its limit. The former is not wrong but I have switched to the latter if that helps.