Answer:
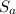 = 2
= 2
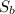
where:
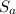 is the sum of the terms in the first sequence, and
is the sum of the terms in the first sequence, and
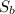 is the sum of the terms in the second sequence.
is the sum of the terms in the second sequence.
Explanation:
The two sequences are arithmetic progression.
From the first sequence,
first term, a = 2
common difference, d = 2
number of terms, n = 5
From the second sequence,
first term, a = 1
common difference, d = 1
number of terms, n = 5
The sum of terms of an arithmetic progression is given as;
=
 [2a + (n - 1) x d]
[2a + (n - 1) x d]
⇒ Let the sum of the first sequence be represented by
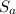 , so that;
, so that;
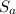 =
=
 [2(2) + (5 - 1) x 2]
[2(2) + (5 - 1) x 2]
=
 [4 + 8]
[4 + 8]
=
 x 12
x 12
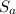 = 30
= 30
⇒ Let the sum of the second sequence be represented by
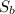 , so that;
, so that;
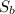 =
=
 [2(1) + (5 - 1) x 1]
[2(1) + (5 - 1) x 1]
=
 [2 + 4]
[2 + 4]
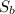 = 15
= 15
Thus, the statement that would correctly describe the relationship between the sequences is;
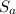 = 2
= 2
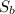
where:
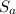 is the sum of the terms in the first sequence, and
is the sum of the terms in the first sequence, and
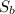 is the sum of the terms in the second sequence.
is the sum of the terms in the second sequence.