Question

Your television picture is created by 480 horizontal lines of pixels, arranged on a screen of total height h. Assume that your ability to resolve the lines is limited only by the Rayleigh criterion, and that the pupils of your eyes are 5.12 mm in diameter. Beyond a certain distance from the screen D, you won't be able to resolve individual lines of pixels and the TV picture will not appear pointillistic. Calculate this ratio D/h of minimum viewing distance to screen height. Assume that the average wavelength of the light coming from the screen is 537 nm.

Answer 1

Ratio D/h of minimum viewing distance to screen height is 16.28

Step-by-step explanation:

Given the data in the question;

Rayleigh criterion sin
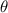`\theta` = 1.22 λ/D

D is diameter (5.12 mm) = 5.12 × 10⁻³

λ is wavelength ( 537 nm) = 537 × 10⁻⁹ m

so we substitute

sin
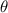`\theta` = 1.22 × 537 × 10⁻⁹ / 5.12 × 10⁻³

sin
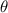`\theta` = 655.14 × 10⁻⁹ / 5.12 × 10⁻³

sin
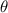`\theta` = 0.000127957

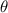`\theta` = sin⁻¹ ( 0.000127957 )

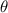`\theta` = 0.007331°

now, tan
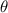`\theta` = y/D

y = h/480

so

tan
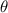`\theta` = h/480 / D

h/D = 480 × tan
`\theta`

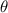
D/h = 1 / ( 480 × tan
`\theta` )

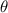we substitute in value of
`\theta`

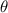
D/h = 1 / ( 480 × tan( 0.007331° ) )

D/h = 1 / ( 480 × 0.00012795 )

D/h = 1 / 0.061416

D/h = 16.28

Therefore, Ratio D/h of minimum viewing distance to screen height is 16.28