Question

Find the maximum rate of change off at the given point and the direction in which it occurs.

f(x, y) = 4y √x, (4, 1)

Answer 1

Maximum rate change |
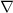`\\abla`f| = √65

Direction = ( 1, 8 ) / √65

i.e Maximum rate change is √65 and it occurs in a direction of ( 1, 8 )

Explanation:

Given that;

f(x, y) = 4y √x, (4, 1)

{ x=4 and y=1 }

Maximum rate of change occurs with the gradient vector;

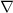`\\abla`f = [ df/dx, df/dy ] = [ 2y/√x, 4√x ]

we substitute in our value of x and y

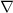`\\abla`f = 2(1)/√4, 4√4

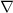`\\abla`f = 2/√4, 4√4

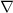`\\abla`f = ( 1, 8 )

Maximum rate change |
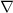`\\abla`f| = | ( 1, 8 ) | = √( 1² + 8² ) = √(1 + 64)

Maximum rate change |
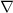`\\abla`f| = √65

Direction =
`\\abla`f / |
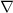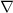`\\abla`f|

we substitute

Direction = ( 1, 8 ) / √65

i.e Maximum rate change is √65 and it occurs in a direction of ( 1, 8 )