Question

At a college campus, random drug tests are carried out to prevent use of prohibited drugs by athletes. Of all the athletes on campus, it is known that 8% use prohibited drugs regularly, 17% use it occasionally; and 75% never use it. The tests which are conducted do not always result in correct diagnosis. Regular prohibited drug users falsely test negative 5% of the time; occasional users falsely test negative 13% of the time; and non-users falsely test positive 11% of the time.

Compute the following:

A. If an athlete is selected at random, what is the probability that athlete will test positive for prohibited drug use?
B. If an athlete tests positive after a drug test, what is the probability that this drug user never used the prohibited drug?

Answer 1

a) 0.3064 = 30.64% probability that athlete will test positive for prohibited drug use.

b) 0.2693 = 26.93% probability that this drug user never used the prohibited drug.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

A. If an athlete is selected at random, what is the probability that athlete will test positive for prohibited drug use?

100 - 5 = 95% of 8%

100 - 13 = 87% of 17%

11% of 75%

So

`p = 0.95*0.08 + 0.87*0.17 + 0.11*0.75 = 0.3064`

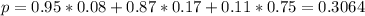
0.3064 = 30.64% probability that athlete will test positive for prohibited drug use.

B. If an athlete tests positive after a drug test, what is the probability that this drug user never used the prohibited drug?

Conditional Probability

Event A: Tests Positive

Event B: Never used the drug.

0.3064 = 30.64% probability that athlete will test positive for prohibited drug use

This means that
`P(A) = 0.3064`

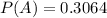
Probability of testing positive while never using the drug.

11% of 75%. So

`P(A \cap B) = 0.11*0.75 = 0.0825`

`P(B|A) = (P(A \cap B))/(P(A)) = (0.0825)/(0.3064) = 0.2693`

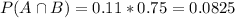
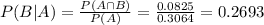
0.2693 = 26.93% probability that this drug user never used the prohibited drug.