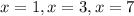Question

11. Solve: (x - 2)(x ^ 2 - 9x + 13) + 5 = 0​

Answer 1

x
3
−9x
2
+13x−2x
2
+18x−26+5=0

Answer 2

`x=1, x=3, x=7`

Explanation:

Start multiplying and adding all together. You get
`x^3-11x^2+31x-21 =0`.

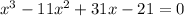At this point we're stuck factoring since there exist a formula for the roots, but it's nowhere easy to remember. We start writing down The List (rational root theorem: it's the divisor of the constant term divided by the divisor of the lead coefficent, with a plus or minus, in our case it's
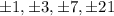`\pm1, \pm3, \pm7, \pm 21`) and let's try checking one by one.

Value
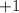`+1` gives a zero on the LHS, it means the polynomial is divisible by
`(x-1)`. By doing the division, or writing it as
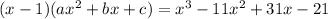`(x-1)(ax^2+bx+c) = x^3-11x^2+31x-21`, multiplying on the LHS and then finding the values of a, b, and c (easiest for me, your mileage may vary) we can write our expression, finally, as

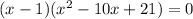`(x-1)(x^2-10x+21) =0` At this point you can either apply the quadratic formula or decompose again the second factor as

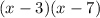`(x-3)(x-7)` by finding two numbers whose sum is -10 and product is 21, ie -3 and -7. At this point the expression

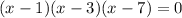`(x-1)(x-3)(x-7)=0` is true if
`x=1, x=3, x=7`