Question

PLEASE SOLVE AND CHECK

Answer 1

`3 {x}^(2) = - 4 + 8x`

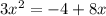
Let us transpose -4 and 8x to the Left Hand Side. So we are left with 0 on the Right Hand Side.

`= > {3x}^(2) + 4 - 8x = 0`

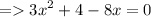
Now, arrange the expression in standard form.

`= > {3x}^(2) - 8x + 4 = 0 \\`

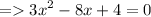
Now, split the mid term. Here, 3 × 4 = 12. So, we can split -8x into -2x and -6x.

`= > ({3x}^(2) - 6x )- (2x + 4) = 0 \\`

Now, take 3x common from the first expression and 2 from the second.

`= > 3x(x - 2) - 2(x - 2) = 0 \\ = > (3x - 2)(x - 2) = 0`

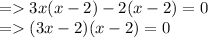
When, two terms are equal to 0, then each term is equal to zero.

`= > 3x - 2 = 0 \: \: and \: x - 2 = 0 \\ = > 3x = 2 \: \: and \: x = 2 \\ = > x = (2)/(3) \: \: and \: \: 2`

Answer:

`x = (2)/(3) \: \: and \: \: 2`

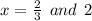
Hope you could understand.

If you have any query, feel free to ask.

Answer 2

x = 2 / 3 or x = 2

Explanation:

3x² = -4 + 8x

3x² - 8x + 4 = 0

3x² - 6x - 2x + 4 = 0

3x ( x - 2 ) -2 ( x - 2 ) = 0

( 3x - 2 ) ( x - 2 ) = 0

Therefore,

3x - 2 = 0 or x - 2 = 0

3x = 2 x = 2

x = 2/3

Hope this helps you :-)