Question

NO LINKS OR ANSWERING QUESTIONS YOU DON'T KNOW!! Chapt 15 part 2a

Explain the process of matrix multiplication. What are the dimensions 9f of the resulting matrix? Use the following matrices for your explanation of the process. AB. Show your work. ​

Answer 1

9514 1404 393

Step-by-step explanation:

Two matrices with dimensions (numbers of (rows, columns)) of (a, b) and (c, d) can only be multiplied if the number of columns in the left matrix is equal to the number of rows in the right matrix. That is, b=c. The dimensions of the product matrix will be (a, d).

For row i of the left matrix and column j of the right matrix, element a(i,j) of the product matrix is the dot-product of row i with column j. (The dot-product of two vectors is the sum of the products of corresponding elements.)

__

The example matrices have (row, column) dimensions (3, 3) and (3, 1), so can be multiplied with a result having dimensions (3, 1).

It is useful to refer to an element of a matrix by specifying the row and column in which it resides. An element of matrix 'A' in row 2 and column 3 can be referred to as A(2,3). Often, subscripts are used, as in ...

`A_(i,j)`

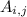
For matrix C = A·B, the element C(1,1) will be the sum ...

A(1,1)B(1,1) +A(1,2)B(2,1) +A(1,3)B(3,1)

Calculators, apps, spreadsheets, and web sites are available that will perform this arithmetic for you. It can be a bit tedious to do by hand.

Here the product is ...

`A\cdot B=\left[\begin{array}{ccc}2&3&-1\\0&2&5\\2&4&0\end{array}\right] \cdot\left[\begin{array}{c}2&1&2\end{array}\right] =\left[\begin{array}{c}2(2)+3(1)+(-1)(2)&0(2)+2(1)+5(2)&2(2)+4(1)+0(2)\end{array}\right] \\\\=\left[\begin{array}{c}5&12&8\end{array}\right]`

Answer 2

We are given the matrices A and B

`A = \left[\begin{array}{ccc}2&3&-1\\0&2&5\\2&4&0\end{array}\right]`

`B = \left[\begin{array}{ccc}2\\1\\2\end{array}\right]`

Multiplying these matrices:

We multiply matrices by taking the first column of the first matrix and the first row of the second matrix

we will multiply all the terms of the first column of the first matrix and multiply them by the terms of the first row of the second matrix, one by one

`AB = \left[\begin{array}{ccc}2(2) + 3(1) + -1(2)\\0(2) + 2(1) + 5(2)\\2(2) + 4(1) + 0(2)\end{array}\right]`

`AB = \left[\begin{array}{ccc}5\\12\\8\end{array}\right]`