Your description of the surface is incomplete. But it looks like you're considering some subset of the paraboloid z = 1 - x ² - y ², so I'll go ahead and assume it's the part of said paraboloid above the x,y-plane, so that the boundary is a circle centered at the origin with radius 1.
By Stokes' theorem, the line integral of F along this boundary (∂S) is equal to the surface integral of curl(F ) over the surface itself (S). We have
F(x, y, z) = z ² i + 2x j + y ² k
which has curl
curl(F ) = (∂(y ²)/∂y - ∂(2x)/∂z) i - (∂(y ²)/∂x - ∂(z ²)/∂z) j + (∂(2x)/∂x - ∂(z ²)/∂y) k
curl(F ) = 2y i + 2z j + 2k
Parameterize S by the vector function,
r(u, v) = u cos(v) i + u sin(v) j + (1 - u ²) k
with 0 ≤ u ≤ 1 and 0 ≤ v ≤ 2π.
Take the upward-pointing normal vector to S to be
n = ∂r/∂v × ∂r/∂u
n = (-u sin(v) i + u cos(v) j ) × (cos(v) i + sin(v) j - 2u k)
n = 2u ² cos(v) i + 2u ² sin(v) j + u k
Then the integral of curl(F ) over S - and hence the line integral of F over ∂S - is
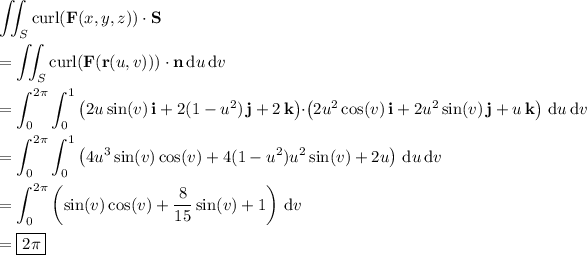
Just to confirm this result, we can compute the line integral directly, since it's not so difficult to deal with. Parameterize ∂S by the vector function
r(t) = cos(t ) i + sin(t ) j
with 0 ≤ t ≤ 2π. (Note that there is a k component, but its coefficient is 0.) Then
dr/dt = -sin(t ) i + cos(t ) j
and the line integral is again
