Answer:
Explanation:
Let's break this down. The secant of a negative angle is the same as the secant of the positive angle. This is because secant is the inverse of cosine, and cosine is an even function. f(-x) = f(x) if the function is even, and f(-x) = -f(x) if the function is odd. Sine is odd and has symmetry about the origin; cosine is even and has y-axis symmetry.
Therefore, sec(-θ) = sec(θ) and we have then
sec(θ) - cos(θ). Since secant is the inverse of cosine, we can write:
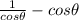 and finding a common denominator:
and finding a common denominator:
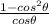 and using a trig identity:
and using a trig identity:
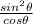 and simplify that down a bit by breaking it up:
and simplify that down a bit by breaking it up:
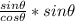 finally boils down to
finally boils down to
tanθ · sinθ, the last choice there.