Question

Solve for x : 2|x-1|+5<13

Answer 1

`Hello`
`There!`

Let's solve your inequality step-by-step.

`2(|x-1|)+5<13`

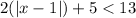
Step 1:

You must add -5 both sides.

`2(|x-1|)+5+-5<13+-5`

`2(|x-1|)<8`

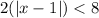
Step 2:

You must divide both sides by 2.

`(2(|x-1|))/(2)`
`\leq (8)/(2)`

`|x-1|<4`

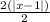
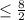
Step 3:

Solve the Absolute Value.

`|x-1|<4`

We know that x−1<4 and x−1>−4.

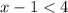`x-1<4` Condition 1.

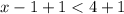`x-1+1<4+1` (Add 1 to both sides)

`x<5`

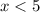
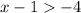`x-1>-4` (Condition 2)

`x-1+1>-4+1` (Add 1 to both sides)

`x>-3`

`ANSWER!`

`x<5`
`and`
`x>-3`

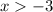
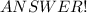
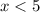
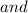
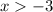
Hopefully, this helps you!!

`AnimeVines`

Answer 2

Hi there!

2|x - 1| + 5 < 13

Begin by subtracting 5 from both sides:

2|x - 1| < 8

Divide both sides by 2:

|x - 1| < 4

Find both the positive and negative solutions:

x - 1 < 4

x < 5

-(x - 1) < 4

-x + 1 < 4

-x < 3

x > -3