Question

A consumer group has determined that the distribution of life spans for gas ranges (stoves) has a mean of 15.0 years and a standard deviation of 4.2 years. The distribution of life spans for electric ranges has a mean of 13.4 years and a standard deviation of 3.7 years. Both distributions are moderately skewed to the right. Suppose we take a simple random sample of 35 gas ranges and a second SRS of 40 electric ranges. Which of the following best describes the sampling distribution of the difference in mean life span of gas ranges and electric ranges?

a. Mean = 1.6 years, standard deviation = 7.9 years, shape: moderately right-skewed.
b. Mean = 1.6 years, standard deviation - 0.92 years, shape: approximately Normal.
c. Mean= 1.6 years, standard deviation = 0.92 years, shape: moderately right skewed.
d. Mean =1.6 years, standard deviation =0.40 years, shape: approximately Normal.
e. Mean =1.6 years, standard deviation =0.40 years, shape: moderately right skewed.

Answer 1

b. Mean = 1.6 years, standard deviation - 0.92 years, shape: approximately Normal.

Explanation:

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

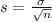For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

Subtraction of normal Variables:

When we subtract normal variables, the mean is the subtraction of the means, while the standard deviation is the square root of the sum of the variances.

A consumer group has determined that the distribution of life spans for gas ranges (stoves) has a mean of 15.0 years and a standard deviation of 4.2 years. Sample of 35:

This means that:

`\mu_G = 15`

`s_G = (4.2)/(√(35)) = 0.71`

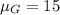
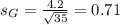
The distribution of life spans for electric ranges has a mean of 13.4 years and a standard deviation of 3.7 years. Sample of 40:

This means that:

`\mu_E = 13.4`

`s_E = (3.7)/(√(40)) = 0.585`

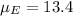
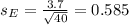
Which of the following best describes the sampling distribution of the difference in mean life span of gas ranges and electric ranges?

Shape is approximately normal.

Mean:

`\mu = \mu_G - \mu_E = 15 - 13.4 = 1.6`

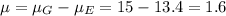
Standard deviation:

`s = √(s_G^2+s_E^2) = √(0.71^2+0.585^2) = 0.92`

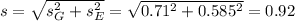
So the correct answer is given by option b.