Answer:
x = y = - 2
Explanation:
Using the rule of radicals/ exponents
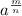 =
=
![\sqrt[n]{a^(m) }](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/gdka8zccyxtzx9p7clsl8f.png) ,
,
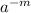 =
=
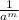 ,
,
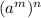 =
=
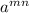
Given
![\sqrt[x]{4}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/ipewrqmtcmqs8g2aaplqpn.png) =
=
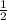 , then
, then
![\sqrt[x]{2^(2) }](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/ln9bjkycmp315gjlkbm1co.png) =
=
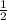
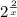 =
=
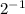
Since the bases on both sides are equal, both 2 , then equate exponents
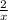 = - 1 ( multiply both sides by x )
= - 1 ( multiply both sides by x )
2 = - x , that is
x = - 2
Similarly
![\sqrt[y]{9}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/7nu2i73zidomtjzrsa78nq.png) =
=
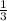 , then
, then
![\sqrt[y]{3^(2) }](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/1dim5qwf28xjffxea3ej7v.png) =
=
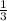
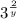 =
=
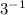
Equating the exponents gives
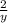 = - 1 ⇒ - y = 2 ⇒ y = - 2
= - 1 ⇒ - y = 2 ⇒ y = - 2