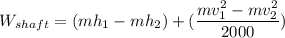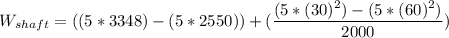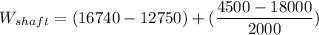Question

A steam turbine generator unit is used to produce electricity, where steam enters the turbine with a velocity of 30 m/s and enthalpy (internal energy) of 3348 kJ/kg. The 1 steam leaves the turbine as a mixture of vapor and liquid having a velocity of 60 m/s and an enthalpy of 2550 kJ/kg. The flow through the turbine is adiabatic, and changes in elevation are negligible. Determine the work output from the turbine, if the mass flow rate is 5kg/s.

Answer 1

3.983 MW

Step-by-step explanation:

Given that:

At the inlet:

Velocity (v₁) = 30 m/s

Enthalpy (h₁) = 3348 kJ/kg

At the outlet:

Velocity (v₂) = 60 m/s

Enthalpy (h₂) = 2550 kJ/kg

Mass flow rate (m) = m₁ = m₂ = 5kg/s

According to the steady flow energy equation:

`Q+ m_1 (h_1 + (v_1^2)/(2000)+ (gz_1)/(1000) )= m_2(h_2+(v_2^2)/(2000)+(gz_2)/(1000))+W_(shaft)`

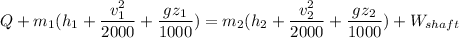
Since the elevation (z) is negligible and flow via the turbine is adiabatic:

Then,

Q = 0 and z₁ = z₂

∴

`W_(shaft) = (mh_1-mh_2) + ((mv_1^2-mv_2^2)/(2000))`

`W_(shaft) = ((5*3348) -(5*2550)) + (((5*(30)^2)-(5*(60)^2))/(2000))`

`W_(shaft) = (16740-12750) + ((4500-18000)/(2000))`

`W_(shaft) = (16740-12750) + (-6.75)`

`W_(shaft) = 3983.25 \ kW`

`\mathbf{W_(shaft) = 3.983 \ MW}`