Question

A sample of 900 computer chips revealed that 61% of the chips fail in the first 1000 hours of their use. The company's promotional literature claimed that under 64% fail in the first 1000 hours of their use. Is there sufficient evidence at the 0.02 level to support the company's claim

Answer 1

The p-value of the test is 0.0301 > 0.02, which means that there is not sufficient evidence at the 0.02 level to support the company's claim.

Explanation:

The company's promotional literature claimed that under 64% fail in the first 1000 hours of their use.

At the null hypothesis, we test if the proportion is of at least 64%, that is:

`H_0: p \geq 0.64`

At the alternative hypothesis, we test if the proportion is of less than 64%, that is:

`H_1: p < 0.64`

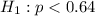
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

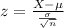
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
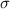`\sigma` is the standard deviation and n is the size of the sample.

64% is tested at the null hypothesis:

This means that
`\mu = 0.64, \sigma = √(0.64*0.36)`

A sample of 900 computer chips revealed that 61% of the chips fail in the first 1000 hours of their use.

This means that
`n = 900, X = 0.61`

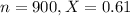
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.61 - 0.64)/((√(0.64*0.36))/(√(900)))`

`z = -1.88`

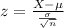
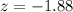
P-value of the test and decision:

The p-value of the test is the probability of finding a sample proportion below 0.61, which is the p-value of z = -1.88.

Looking at the z-table, z = -1.88 has a p-value of 0.0301.

The p-value of the test is 0.0301 > 0.02, which means that there is not sufficient evidence at the 0.02 level to support the company's claim.